📌 문제
색을 표현하는 기본 요소를 이용하여 표시할 수 있는 모든 색 중에서 대표적인 색을 고리 모양으로 연결하여 나타낸 것을 색상환이라고 한다. 미국의 화가 먼셀(Munsell)이 교육용으로 고안한 20색상환이 널리 알려져 있다. 아래 그림은 먼셀의 20색상환을 보여준다.
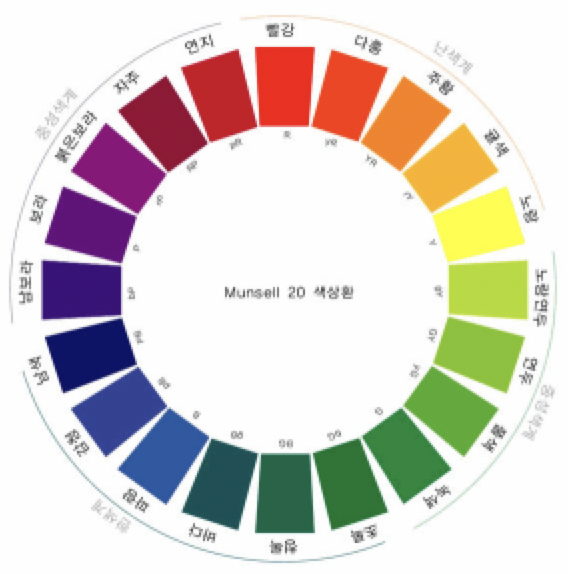
그림 1. 먼셀의 20색상환
색상환에서 인접한 두 색은 비슷하여 언뜻 보면 구별하기 어렵다. 위 그림의 20색상환에서 다홍은 빨강과 인접하고 또 주황과도 인접하다. 풀색은 연두, 녹색과 인접하다. 시각적 대비 효과를 얻기 위하여 인접한 두 색을 동시에 사용하지 않기로 한다.
주어진 색상환에서 시각적 대비 효과를 얻기 위하여 서로 이웃하지 않은 색들을 선택하는 경우의 수를 생각해 보자. 먼셀의 20색상환에서 시각적 대비 효과를 얻을 수 있게 10개의 색을 선택하는 경우의 수는 2이지만, 시각적 대비 효과를 얻을 수 있게 11개 이상의 색을 선택할 수 없으므로 이 경우의 수는 0이다.
주어진 정수 N과 K에 대하여, N개의 색으로 구성되어 있는 색상환 (N색상환)에서 어떤 인접한 두 색도 동시에 선택하지 않으면서 서로 다른 K개의 색을 선택하는 경우의 수를 구하는 프로그램을 작성하시오.
📌 입력
입력 파일의 첫째 줄에 색상환에 포함된 색의 개수를 나타내는 양의 정수 N(4 ≤ N ≤ 1,000)이 주어지고, 둘째 줄에 N색상환에서 선택할 색의 개수 K(1 ≤ K ≤ N)가 주어진다.
📌 출력
첫째 줄에 N색상환에서 어떤 인접한 두 색도 동시에 선택하지 않고 K개의 색을 고를 수 있는 경우의 수를 1,000,000,003 (10억 3) 으로 나눈 나머지를 출력한다.
📌 문제 풀이
👨🏫 접근
재귀를 통해 문제를 풀고자 했으나 워낙 시간 복잡도가 클 것 같아서 dp를 통해서 문제를 풀이했다.
첫 번째로 생각한 것은 for문으로 idx를 모두 순회하면서 풀이했었는데, 이 경우 시간이 오래 걸리는 건 매한가지라는 점 때문에 실패했다.
두 번째는 현재의 인덱스 색상을 선택할지 선택하지 않을지를 선택하는 것이다. 시작하는 인덱스를 n이라고 한다면, n - 1번째 인덱스 색상으로 이동한다거나 n - 2번째 인덱스 색상을 선택하고 그 인덱스 색상으로 이동하는 것이다.
예를 들어 현재 10번째 색을 검사하는 과정일 때, 9번째 색으로 이동하거나 8번째 색상을 선택하고 8번째 색상을 주목하는 상태에서 동일한 검사를 진행하는 것이다.
이때 그냥 이전 색으로 이동하는 것은 현재의 색상과 이웃하는 색상은 고르지 못하기 때문에 다음 색상은 고르지 않고 포커스 지점을 이동시키는 것이다.
색상이 9개인 경우 10개의 테이블을 준비한다. 그리고 시작은 10번 인덱스에서 시작한다. 10번 인덱스는 문제 풀이를 위해 만든 인덱스로 신경쓰지 않고 위의 과정을 진행한다.
- 이전 인덱스로 이동하는 경우
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
10번 인덱스로부터 9번 색상은 아직 남은 기회가 n번 있고, 8번 색상은 남은 기회가 n - 1번 있다.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
그 다음 9번 색상을 포커스를 둔 후, 8번 색상은 n번의 기회가 있고, 7번 색상은 n - 1번의 기회가 있다.
이런식으로 계속 이동하다가 0번 인덱스 혹은 1번 인덱스를 마주하면 값을 출력하기 시작한다. 일단 기본적으로 아무 것도 선택하지 않은 상황은 그 테이블 값을 1로 초기화 해준다. 식으로 나타내면 d[i][0] = 1이다. 그리고 선택을 한 번 한 상황은 그 테이블 값을 그 색상의 인덱스로 초기화한다. d[i][1] = i
그 이유는 색상을 고르지 않았다는 것은 모든 색상이 완료되었을 때 가능한 경우의 수임을 반환하기 위함이며, 선택을 한 번 했다는 것은 사실 그 색상으로부터 그 이전 색상을 한 번씩 모두 고를 수 있다는 것이기 때문에 총 n개의 경우의 수가 생긴다. 6개의 색상에서 1개의 색상을 찾는 경우의 수를 생각해보면 이해할 수 있다.
솔직히 설명하기 좀 어려운 것 같다 ㅠ
👨🏫 문제 풀이
📄 전체 코드
n = int(input())
k = int(input())
mod = 1000000003
# k번 선택했을 때의 n번째 인덱스가 가질 수 있는 경우의 수
d = [[-1] * (k + 1) for _ in range(n + 1)]
for i in range(n + 1):
d[i][0] = 1
d[i][1] = i
def find_color(n, k):
if k > n / 2:
d[n][k] = 0
return 0
if d[n][k] != -1:
return d[n][k]
else:
d[n][k] = find_color(n - 1, k) % mod + find_color(n - 2, k - 1) % mod
return d[n][k] % mod
print(find_color(n, k))📄 준비
n = int(input())
k = int(input())
mod = 1000000003
# k번 선택했을 때의 n번째 인덱스가 가질 수 있는 경우의 수
d = [[-1] * (k + 1) for _ in range(n + 1)]
for i in range(n + 1):
d[i][0] = 1
d[i][1] = i📄 풀이
def find_color(n, k):
if k > n / 2:
d[n][k] = 0
return 0
if d[n][k] != -1:
return d[n][k]
else:
d[n][k] = find_color(n - 1, k) % mod + find_color(n - 2, k - 1) % mod
return d[n][k] % mod
print(find_color(n, k))선택할 수 있는 수가 n / 2보다 크다면 절대 가능하지 않기 때문에 d[n][k]를 0으로 갱신한다. 6개의 색상에서 4개의 색을 선택하는 경우의 수를 생각해보면 불가능함을 알 수 있다.
📌 총평
어렵네 ^^,,

'Algorithm > Dynamic Programming' 카테고리의 다른 글
| [Python - Dynamic Programming] 11054 가장 긴 바이토닉 부분 수열 (1) | 2022.12.25 |
|---|---|
| [Python - Dynamic Programming] 2225 합분해 (0) | 2022.09.27 |
| [Python - Dynamic Programming] 11048 이동하기 (0) | 2022.09.25 |
| [Python - Dynamic Programming] 11660 구간 합 구하기 5 (1) | 2022.09.23 |
| [Python - Dynamic Programming] 9657 돌 게임 3 (1) | 2022.09.23 |
