📌 문제
세 개의 장대가 있고 첫 번째 장대에는 반경이 서로 다른 n개의 원판이 쌓여 있다. 각 원판은 반경이 큰 순서대로 쌓여있다. 이제 수도승들이 다음 규칙에 따라 첫 번째 장대에서 세 번째 장대로 옮기려 한다.
- 한 번에 한 개의 원판만을 다른 탑으로 옮길 수 있다.
- 쌓아 놓은 원판은 항상 위의 것이 아래의 것보다 작아야 한다.
이 작업을 수행하는데 필요한 이동 순서를 출력하는 프로그램을 작성하라. 단, 이동 횟수는 최소가 되어야 한다.
아래 그림은 원판이 5개인 경우의 예시이다.

📌 입력
첫째 줄에 첫 번째 장대에 쌓인 원판의 개수 N (1 ≤ N ≤ 20)이 주어진다.
📌 출력
첫째 줄에 옮긴 횟수 K를 출력한다.
두 번째 줄부터 수행 과정을 출력한다. 두 번째 줄부터 K개의 줄에 걸쳐 두 정수 A B를 빈칸을 사이에 두고 출력하는데, 이는 A번째 탑의 가장 위에 있는 원판을 B번째 탑의 가장 위로 옮긴다는 뜻이다.
📌 문제 풀이
👨🏫 접근
대표적인 재귀 문제이다. 솔직히 이걸 보고 어떻게 재귀를 떠올릴 수 있을까 싶은데, 자세히 보면 어느 정도 규칙성이 있다.

이렇게 하노이의 탑이 있다고 할 때, 가장 아래 원판이 타워 3으로 가야 한다. 그렇기 때문에 1, 2 크기 원판을 타워 2로 보낸다.

그런 다음 타워 1에 있는 원판을 타워 3으로 이동시킨다.

그 이후 타워 2에 있는 것들을 타워 3에 모두 옮기면 된다.

이러한 과정은 원판이 4개일 때에도 동일하다.

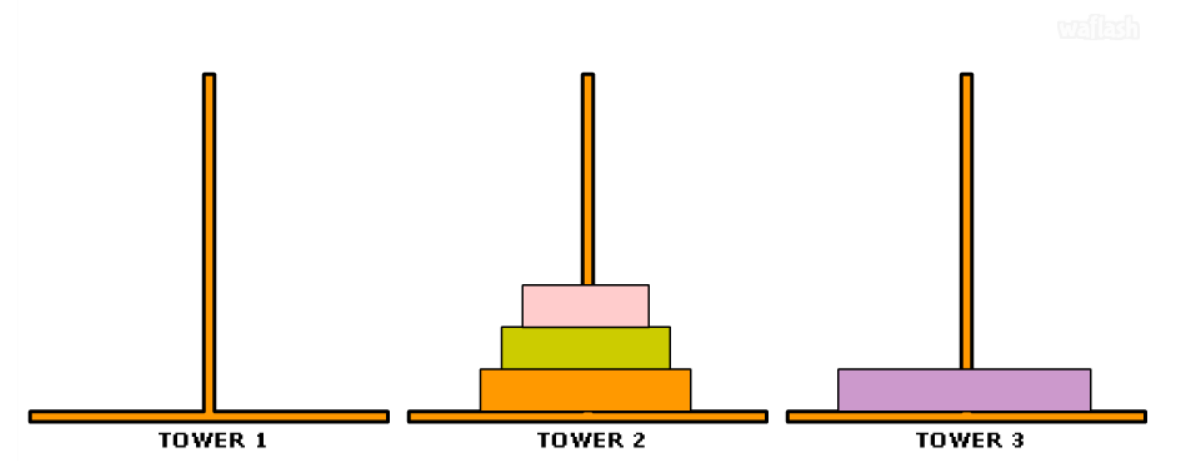

전체적인 과정은 이러하다.
n - 1개의 원판을 2번 타워에 옮기고, n 원판을 3번 타워로 이동시키며, n - 1 개의 원판을 3번 타워로 이동시킨다.
가장 아래에 있는 원판은 사실 없는 것과 비슷한 상태이다. 다른 말로 하면 바닥과 같다는 의미이다. 그래서 n - 1개의 원반이 자유롭게 이동할 수 있는 것이다.
원판을 옮길 수 있는 과정은
- n 원판을 제외하고 나머지 원판들을 두 번째 타워로 옮긴다.
- n 원판을 세 번째 타워로 옮긴다.
- 나머지 원판들을 세 번째 타워로 옮긴다.
더 자세히 분석해보도록 하자.
- 1 번을 하기 위해서 n - 1개의 원판은 첫 번째 타워를 시작으로 하여 세 번째 타워를 거쳐 두 번째 타워로 이동한다.
- 2 번을 하기 위해서 따로 두 번째 원판을 거치지 않고 세 번째 타워로 이동한다.
- 3 번을 하기 위해서 n - 1개의 원판은 두 번째 타워를 시작으로 하여 첫 번째 타워를 거쳐 세 번째 타워로 이동한다.
이제 이것을 코드로 구현하면 된다.
👨🏫 문제 풀이
📄 전체 코드
n = int(input())
def hanoi(n, start, to, end):
if n == 1:
print(start, end)
else:
hanoi(n - 1, start, end, to)
print(start, end)
hanoi(n - 1, to, start, end)
print(2 ** n - 1)
hanoi(n, 1, 2, 3)📄 준비
n = int(input())크게 준비할 것은 없다.
📄 풀이
def hanoi(n, start, to, end):
if n == 1:
print(start, end)
else:
hanoi(n - 1, start, end, to)
print(start, end)
hanoi(n - 1, to, start, end)
print(2 ** n - 1)
hanoi(n, 1, 2, 3)하노이의 탑이 1번 타워에서 2번 타워를 거쳐 3번 타워로 이동하는 순서로 이동하도록 인자를 넣었다.
재귀함수의 시간 복잡도는 2n이며 n == 1일 때는 hanoi 함수를 2번 호출하지 않고 한 번만 호출하기 때문에 2n-1을 해주도록 한다.
start 매개변수는 원판 덩어리(혹은 원판 1개)의 처음 위치이며, to는 end로 가기 위해 거쳐가는 지점이고, end는 최종적으로 도달할 곳이다.
n == 1일 때, 마지막 1번 원판이 남았을 때 중간을 거칠 필요 없이 바로 end로 거쳐가면 되므로 print(start, end)를 출력한다.
n != 1일 때, 즉 원판 덩어리일 때의 조건을 보도록 하자. 앞서 접근에서 원판을 이동시켰던 과정에 맞춰서 함수를 호출한다. n - 1개의 원판을 두 번째 타워로 옮기고, n 원판을 세 번째 타워로 옮긴 다음 나머지 n - 1개의 원판을 세 번째 타워로 옮긴다.
이러한 과정을 거쳐 최종적으로 모든 하노이의 원판을 옮길 수 있게 된다.
📌 총평
여전히 완벽한 이해는 되지 않으나 정말 알고리즘을 간결하게 하고 구현 능력을 기르는 데 좋은 게 재귀인 것 같다.

'Algorithm > Recursion & Backtracking' 카테고리의 다른 글
| [Python] 1182 부분 수열의 합 (0) | 2022.06.22 |
|---|---|
| [Python] 14888 연산자 끼워넣기 (0) | 2022.06.22 |
| [Python] 15666 N과 M(12) (0) | 2022.06.12 |
| [Python] 15665 N과 M(11) (0) | 2022.06.12 |
| [Python] 15664 N과 M(10) (0) | 2022.06.11 |