📌 문제
경비행기 독수리호가 출발지 S에서 목적지 T로 가능한 빠른 속도로 안전하게 이동하고자 한다. 이때, 경비행기의 연료통의 크기를 정하는 것이 중요한 문제가 된다. 큰 연료통을 장착하면 중간에 내려서 급유를 받는 횟수가 적은 장점이 있지만 연료통의 무게로 인하여 속도가 느려지고, 안정성에도 문제가 있을 수 있다. 한편 작은 연료통을 장착하면 비행기의 속도가 빨라지는 장점이 있지만 중간에 내려서 급유를 받아야 하는 횟수가 많아지는 단점이 있다. 문제는 중간에 내려서 급유를 받는 횟수가 k이하 일 때 연료통의 최소용량을 구하는 것이다. 아래 예를 보자.
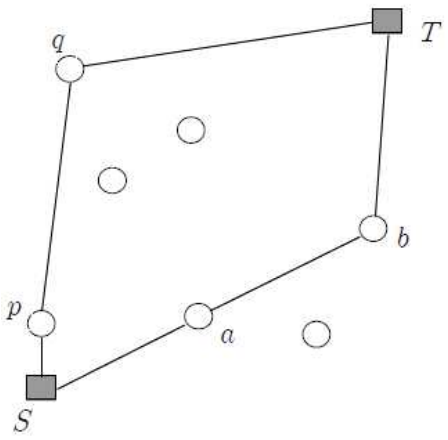
위 그림은 S, T와 7개의 중간 비행장의 위치를 나타내고 있는 그림이다. 위 예제에서 중간급유를 위한 착륙 허용 최대횟수 k=2라면 S-a-b-T로 가는 항로가 S-p-q-T로 가는 항로 보다 연료통이 작게 된다. 왜냐하면, S-p-q-T항로에서 q-T의 길이가 매우 길어서 이 구간을 위해서 상당히 큰 연료통이 필요하기 때문이다. 문제는 이와 같이 중간에 최대 K번 내려서 갈 수 있을 때 최소 연료통의 크기가 얼마인지를 결정하여 출력하면 된다. 참고사항은 다음과 같다.
- 모든 비행기는 두 지점 사이를 반드시 직선으로 날아간다. 거리의 단위는 ㎞이고 연료의 단위는 ℓ(리터)이다. 1ℓ당 비행거리는 10㎞이고 연료주입은 ℓ단위로 한다.
- 두 위치간의 거리는 평면상의 거리이다. 예를 들면, 두 점 g=(2,1)와 h=(37,43)간의 거리 d(g,h)는 $\sqrt{(2-37)^{2} + (1 - 43)^{2}}$ = 54.671... 이고 50<d(g,h) ≤ 60이므로 필요한 연료는 6ℓ가 된다.
- 출발지 S의 좌표는 항상 (0,0)이고 목적지 T의 좌표는 (10000,10000)으로 모든 입력 데이터에서 고정되어 있다.
- 출발지와 목적지를 제외한 비행장의 수 n은 3 ≤ n ≤ 1000이고 그 좌표 값 (x,y)의 범위는 0<x,y<10000의 정수이다. 그리고 최대 허용 중간급유 횟수 k는 0 ≤ k ≤ 1000이다.
📌 입력
첫 줄에는 n과 k가 하나의 공백을 사이에 두고 주어진다. 그 다음 n개의 줄에는 각 비행장 (급유지)의 정수좌표가 x y 형식으로 주어진다.
📌 출력
S에서 T까지 k번 이하로 중간급유 하여 갈 수 있는 항로에서의 최소 연료통 용량에 해당되는 정수를 출력한다.
📌 문제 풀이
👨🏫 접근
두 번째로 파라메트릭 서치와 BFS를 연결하여 풀었던 문제이다. 매개변수 탐색이라고 생각했던 부분은 일단 연료통의 범위가 매우 넓었다. 여기서 n의 범위는 1000까지이고 1~1415 의 연료통을 사용하기 때문이다. 그래서 매개 변수를 통한 이분 탐색으로 적합한 연료통을 찾아내야 한다.
이때, 각 중간 급유소에서 목적지까지 이동하는 과정이 필요해서 그래프 탐색을 해야 했다.
👨🏫 문제 풀이
📄 전체 코드
from collections import deque
import sys
import math
input = sys.stdin.readline
# 기준은 연료통으로
def calc(c1, c2):
return (c1[0] - c2[0]) ** 2 + (c1[1] - c2[1]) ** 2
def bfs(cur, cnt):
q = deque([(cur, cnt)]) # 처음부터 시작, k = 0
visited = [False] * (n + 2)
visited[0] = True
while q:
idx, cnt = q.popleft()
if idx == n + 1:
return True
if cnt > k:
continue
for i in range(1, n + 2):
if cnt <= k and not visited[i]:
if dist[idx][i] <= cost:
visited[i] = True
q.append((i, cnt + 1))
return False
n, k = map(int, input().split())
graph = [[0, 0]] + [list(map(int, input().split()))
for _ in range(n)] + [[10000, 10000]]
ans = 0
dist = [[0] * (n + 2) for _ in range(n + 2)]
for i in range(n + 1):
for j in range(i, n + 2):
if i == j:
dist[i][j] = float('inf')
else:
dist[i][j] = dist[j][i] = calc(graph[i], graph[j])
# 최소, 최대 연료통
pl, pr = 1, 1415
while pl <= pr:
mid = (pl + pr) // 2
cost = mid ** 2 * 100
if bfs(0, 0):
pr = mid - 1
ans = mid
else:
pl = mid + 1
print(ans)📄 준비
from collections import deque
import sys
import math
input = sys.stdin.readline
# 기준은 연료통으로
def calc(c1, c2):
return (c1[0] - c2[0]) ** 2 + (c1[1] - c2[1]) ** 2
...
n, k = map(int, input().split())
graph = [[0, 0]] + [list(map(int, input().split()))
for _ in range(n)] + [[10000, 10000]]
ans = 0
dist = [[0] * (n + 2) for _ in range(n + 2)]
for i in range(n + 1):
for j in range(i, n + 2):
if i == j:
dist[i][j] = float('inf')
else:
dist[i][j] = dist[j][i] = calc(graph[i], graph[j])
# 최소, 최대 연료통
pl, pr = 1, 1415
...
print(ans)연산을 많이 수행할 예정이라서 두 좌표의 길이를 구하는 식은 따로 함수로 정의했다. 루트를 씌우지 않은 이유는 하나하나 루트 연산을 다 하다보면 너무 시간 소요가 컸기 때문이다. 그 이후 모든 항로의 입력을 받고, 각 항로를 양방향 간선으로 설정해주었다. 그리고 최소 연료통은 1로 최대 연료통은 1415로 설정했는데, 중간 급유 없이 출발부터 끝까지 간다고 할 때 필요한 최소 연료통이 1415L였기 때문이다.
📄 풀이
def bfs(cur, cnt):
q = deque([(cur, cnt)]) # 처음부터 시작, k = 0
visited = [False] * (n + 2)
visited[0] = True
while q:
idx, cnt = q.popleft()
if idx == n + 1:
return True
if cnt > k:
continue
for i in range(1, n + 2):
if cnt <= k and not visited[i]:
if dist[idx][i] <= cost:
visited[i] = True
q.append((i, cnt + 1))
return False
while pl <= pr:
mid = (pl + pr) // 2
cost = mid ** 2 * 100
if bfs(0, 0):
pr = mid - 1
ans = mid
else:
pl = mid + 1
print(ans)연산의 복잡도를 줄이기 위해서 mid를 구하여 cost 변수에 값을 저장했다. 이 cost가 연료통 연산에 사용된다. 만약 그 연료통을 충족시킨다면 연료통을 더 줄여서 테스트하기 위해서 pr을 이동시킨다. ans에 값을 같이 저장한다.
📌 총평
처음에 다 풀어보고 다른 사람의 풀이에서 루트 연산을 없애고 풀어보았더니 파이썬 제출에서 1등이었다. 처음 1등이라 좀 신기했다.

'Algorithm > Binary Search' 카테고리의 다른 글
| [Python - Binary Search] 3079 입국심사 (0) | 2022.09.13 |
|---|---|
| [Python - Binary Search] 2110 공유기 설치 (0) | 2022.09.04 |
| [Python - Binary Search] 2512 예산 (0) | 2022.09.04 |
| [Python - Binary Search] 1654 랜선 자르기 (0) | 2022.09.04 |
| [Python - Binary Search] 2805 나무 자르기 (0) | 2022.09.04 |
